Råde-design.

Krefter som virker på råden.

• Krefter på stempel pga sylindertrykk under forbrenning og treghetsmomentet til de bevegelige delene.
• Krefter pga treghetsmomentet til råde, eller bøyemoment.
• Krefter pga friksjon

Rent designmessig er det et par geometriske størrelser som teller:

• Dimensjonene på det kryssende arealet på råden. Hvorfor er råden ofte rektangulær i sin ytre form?
• Dimensjonene til rådens lagertapp på lille og store ende
• Dimensjonering av rådebolter.

Hvor mye tåler råden?

Kompressive krefter.

• Kompressive krefter fra trykket som oppstår i forbrenningsprosessen.
  Kraften på stempel kan vi se på pascals lov for trykk der p trykk = Fkraft/Areal stempel.
  Noteres som p=F/As. Med denne loven kan vi observere at stempelkraften F=pA. Dvs kraften som virker på stempel er produktet av sylindertrykket og stempelarealet.
  Fra termodynamikken kan vi bruke prosess og tilstandsligning for å regne oss frem til forbrenningstrykk når vi vet massefløde til motoren.

Vi kan også «gjette» oss frem til kraften ved å bruke motoreffekt som utgangspunkt.

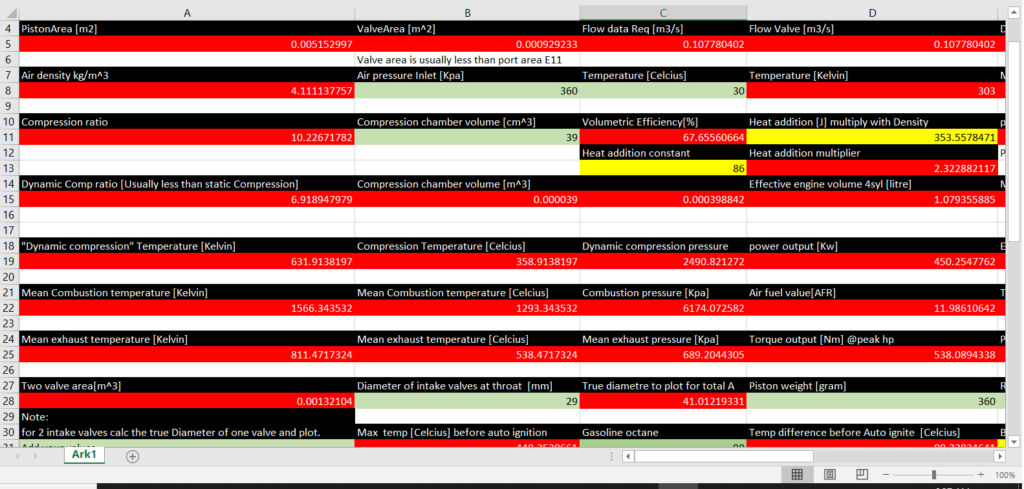
• Jeg bruker et utregningsark på 140 celler som jeg har utviklet til beregninger av blant annet sylindertrykk. Denne har elementer fra Termodynamikk, Fluidmekanikk og maskinlære.

Stålets egenskaper:
Diagram for materialflyt for stål ser slik ut:

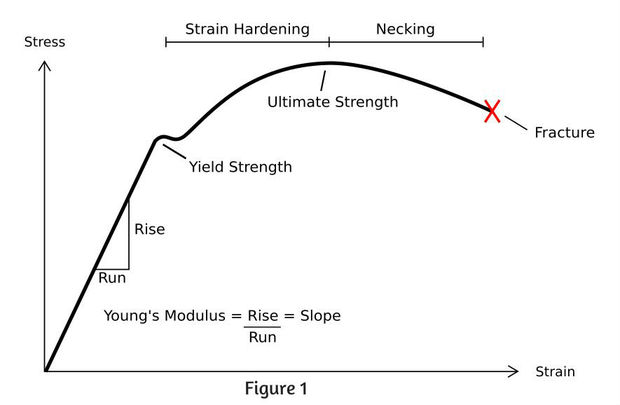
Når man designer en råde settes en sikkerhetsfaktor mot materialflyt på ca 5.
Flytegrensen er det området der metallet går fra elastisk formasjon til plastisk deformasjon.
Det vil si formen på metallet endres og stykket arbeids herdes. For å unngå en endring egenskaper som kan føre til brudd vil man typisk holde de påtrykte kreftene et godt stykke under flytegrensen.
Typisk stålstyrke for en smidd råde av typen 4043 Chm er 145000psi, eller ca 1000Mpa

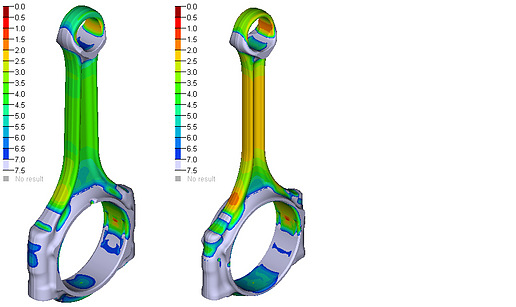
Hva tåler råden:
Først er det viktig å nevne at den beste målemetoden er en kraftmaskin som kan sette last på den valgte råde og måle når deformasjon inntreffer. Både i strekk og trykk kraftretning.
Det krever at man kjøper 2 råder som da ødelegges.

Det nest beste er å utføre numeriske beregninger. Det er ofte billigere og raskere og består av håndberegninger og en FEM analyse. Dvs et dataprogram som beregner styrke ift struktur. Jeg liker å kalle dette en 3 dimensjonal analyse.

Man kan også gjette seg litt frem til styrke ved å ta tverrsnittet av rådens minsteareal rett over store enden. Fra stempelkraften beregner man stress påkjenninger på råden og ser om man er innenfor sikkerhetsmarginen på 5.
Dette kaller jeg en 1 dimensjonal analyse, eller intelligent gjetting.
 
Først ser man på trykk kreftene på stempelet som overføres til råden. Disse gir utslag som et bøyemoment på råden, og rådens geometri beregnes utfra dette. Der er elementer som “Andre arealmoment”, rådelengde, stålkonstanter som påvirker rådens design.

Når man skal beregne hvilke krefter som virker på råden betrakter man systemet og geometrien. Siden dette ikke er en design artikkel, men mer en beregning kan man betrakte de størrelsene man har å jobbe med.

Kraften som virker på råden henter vi fra ligning:
P=Pc*cosø, som forteller at kraften synker med veiv vinkel. mhp rotasjonen til veiva.

Omrokkerer:
Pc=P/cosø, Største kraft fremtrer ved veiv vinkel ca 3.3grader .
Cosø = cos3.3= 0.998 er tilnærmet lik 1

Setter derfor Pc = P. kraften på stempel er lik maksimalkraften på råden.
En illustrasjon av figur her:

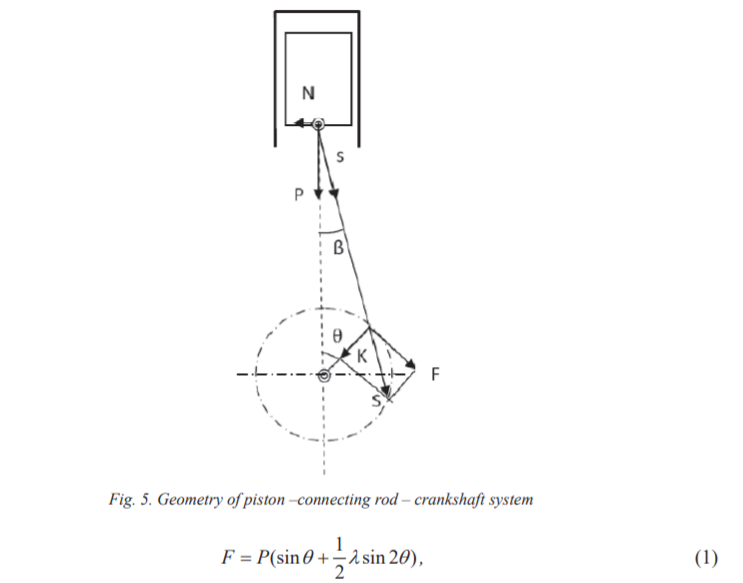
Eksempel:

Standard motor med forbrenningstrykket 15.73bar i en sylinder. Type L4 ca 160hk på 8100rpm i motor.

Montert inn en smidd råde med et tverrsnittareal på 190mm^2

Stress på råde:
Først finner man kraften fra Pascals lov og Stempelarealet ved arealet på en sirkel pi/4*D^2
P=F/A-> F=p*A setter sikkerhetsfaktor fs=5. stempeldiameter D er 81mm

Så kraften som virker på råden som følge av trykk og stempelareal:

Scr=pmaks*As

F= Scr=P3*A = 1.573Mpa(pi/4*81^2) = 8105,6N

Stresset på råden:
Vi bruker nok en gang pascals lov P=F/A og sier:
stress S = F/A, legger til sikkerhetsfaktor på fs = 5

S = fs*F/A = (5*8105,6N)/190mm^2 = 213N/mm^2

S maks for 4340 Chm = 1000Mpa.
1000N/mm^2/213N/mm^2 = 4.69.

Så man kan se at disse rådene er overdimensjonerte I forhold til motorkraften.

Neste eksempel:
Vi kan legge til en turbo og anta at den økte effekten KUN kommer som konsekvens av økt sylindertrykk.

Trykk inn i motor økes fra 95kpA inn i innsug til 360kpA
Dvs vi øker trykket fra svakt atmosfærisk til 2.6bar overtrykk. Alle forutsetninger er tilstede og motoreffekten øker fra 160 til 612hk.
Forbrenningstrykket øker fra 15.7bar til 62bar

Scr=pmaks*As

Scr=P3*A = 6.2Mpa*pi/4*81^2

Scr= 31948N

Stresset på råden:
Vi bruker nok en gang pascals lov P=F/A og sier:
stress S = F/A, legger til sikkerhetsfaktor på fs = 5

S= fs*F/A = 5*31948N/190mm^2 = 841N/mm^2

S maks for 4340 Chm = 1000Mpa.
1000N/mm^2/841N/mm^2 = 1.1894.

Fra beregningene kan vi se at L4 konfigurasjon med disse rådene vil fint takle 612hk.
Ikke glem at vi har en sikkerhetsfaktor på 5 også. 
                                                                          Bøyd råde som følge av sylindertrykk

Vi kan konkludere med at for å øke kapasiteten til råden må vi enten øke flate arealet, eller øke maks tillatt stress før flyt ved å bruke et annet materiale. Det er viktig å huske på at de oscillerende krefter øker proporsjonalt med øking av masse. Og en større råde vil også bli tyngre.